优游国际

KOMPAS.com - Induksi matematika adalah metode pembuktian yang sering digunakan untuk menentukan kebenaran dari suatu pernyataan yang diberikan dalam bentuk bilangan asli.

Dilansir dari buku Peka Soal Matematika (2020) oleh Darmawati, pembuktian dengan induksi matematika memiliki tiga langkah berikut:

1. Tunjukkan bahwa pernyataan benar untuk n = 1
2. Asumsikan pernyataan benar untuk n = k
3. Tunjukkan bahwa n = k+1 juga benar

Baca juga: Apa itu Induksi Matematika?

Jika ketiga langkah benar, maka dapat disimpulkan pernyataan benar untuk setiap n bilangan asli.

Terdapat beberapa pernyataan yang berhubungan dengan bilangan asli yang dapat dibuktikan dengan induksi matematika.

Pernyataan yang dimaksud adalah model induksi matematika berupa barisan, ketidaksamaan, dan keterbagian.

Dikutip dari buku Intisari & Bank Soal Supermath SMA/MA (2018) oleh Tim Supermath, berikut contoh soal dan pembahasan mengenai induksi matematika:

Baca juga: Contoh Soal Induksi Matematika

Contoh soal 1

Misalnya akan dibuktikan untuk semua bilangan asli n bahwa:

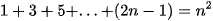
Jawab:

Pertama, kita akan membuktikannya secara berurutan.

• Akan dibuktikan rumus benar untuk n=1

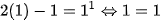...benar

Baca juga: Contoh Soal Induksi Matematika n<2^n

• Andaikan rumus benar untuk n=k

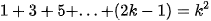...benar

• Akan dibuktikan rumus benar untuk n=k+1

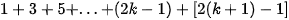
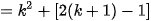
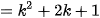
...benar

Jadi, rumus berlaku untuk semua bilangan asli n.

Baca juga: Contoh Soal Pembuktian Induksi Matematika

Contoh soal 2

Buktikan bahwa untuk setiap bilangan asli n berlaku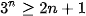

Jawab:

Pertama, kita lakukan pembuktian secara berurutan.

• Ditunjukkan untuk n=1 benar

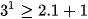
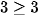
Jadi, pernyataan benar untuk n=1

Baca juga: Contoh Soal Induksi Matematika 2^n>2n untuk Setiap n Bilangan Asli

• Misalkan pernyataan benar untuk n=k. Diperoleh
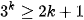
• Akan dibuktikan bahwa n=k+1 benar

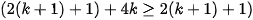
Karena semua langkah benar, berarti terbukti bahwa untuk setiap bilangan asli n berlaku

Itulah penjelasan mengenai pembuktian menggunakan 3 langkah induksi matematika.